Logic gates in Quantum Computing

 A computer comprises of two components: hardware and software. 

Computer hardware refers to the physical components of a computer system, such as the central processing unit (CPU), memory, hard drive, motherboard, and peripherals like keyboards, mice, and monitors. Hardware components work together to allow the computer to function properly and carry out tasks according to software instructions. Hardware can be upgraded, replaced, or repaired, and it can be manufactured by various technology companies. Hardware can range from personal computers and laptops to servers, mobile devices, and other electronic equipment. 

Computer software refers to a collection of instructions or programs that are designed to perform specific tasks on a computer system. This can include operating systems, applications, utilities, and games. Software is what enables users to interact with and make use of the hardware, and it can be written in various programming languages. Software can be installed, updated, and uninstalled on a computer system, and it can be developed by individuals, organizations, or software companies. 

Next is a video that further explains these two components.

Classical Gates- The "NOT" Gate

We just learned about bits. Bits can be stored using anything that can take two different values, like 0 or 1, or up or down, blue or yellow, etc.  

But what are bits? How are they made? How do we distinguish between a 1 bit and 0 bit? Fundamentally, bits are just our interpretation of electricity moving through wires or being stored on a component. We set a threshold for a given part of the circuit and measure the current or voltage. If the measured value is higher than that threshold, we call it 1, and if it's lower we call it 0. There are other ways that we can describe the same process. 

The 1 bit can also be described as an arrow pointing upwards, or a "true" statement, while the 0 bit can be described with a downward arrow or a "false" statement. When we want to change a bit in some way, we pass it through a gate.  

 Gates are logic statements like NOT, OR, AND, etc. You may not know it, but we use logic gates all the time. Here is an example:  

"I have a sweater, so I am not cold". 

 The "not" in this sentence is the gate. You can break it down into smaller pieces of information and ask if each one is true or false.  

Do I have a sweater? True.

 Am I cold? False. 

 We can also change examine the other possible case: 

 Do I have a sweater? False.  

Am I cold? True.   

In this case, the two statements have to be opposites. If the first part is true, the second part must be false, and vice versa.   

Computers also have a NOT gate! It has exactly the same function as "not" in speech.    

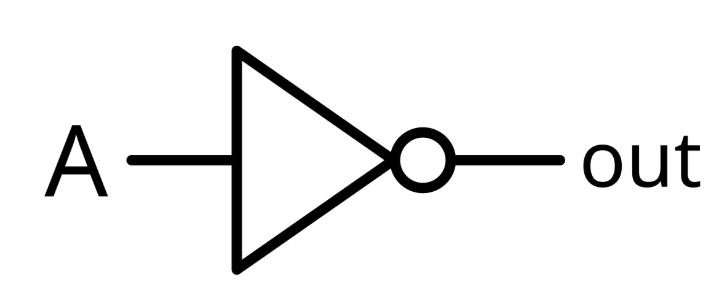
The NOT gate changes 0 to 1, and 1 to zero. This gate is usually shown as the symbol below. The NOT gate only takes one input. The input is shown on the left side and the output on the right side.

For example, when the NOT gate is applied on a bit with the value 1, the output will be 0 (and vice versa):

Or equally when the input to a NOT gate is true, the output will be false:

Classical Gates- The "AND" Gate

The next gate we are going to discuss is called the AND gate. Just like the NOT gate, we use "and" logic in conversation. The "and" gates needs all of the input statements to be true for the result to be true. Let's start with an example of how it works in speech, and then take a look at the same operation for a computer.  

"If you walked the dog, and loaded the dishwasher, and finished your homework, you can go to the movies with your friends". 

 Now we can break down each piece:

 

Did you walk the dog? True.  

Did you load the dishwasher? True. 

Is your homework done? True. 

Then it is TRUE that you can go to the movies!   

However, if any of the three statements are FALSE, then you won't be able to go to the movies.  

For computers, it works exactly the same way.   

Unlike the NOT gate, which would take only a single input, the AND gate takes in at least 2 inputs. The output of the AND gate is equal to 1 only when all the inputs are equal to 1. That means even if just one of the inputs is zero the rest does not matter and the output will surely be zero. You can see the symbol for the AND gate with 2 inputs below:

As we discussed before, we can describe bits using True/False. Doing this, we get the following truth table. 

Classical Gates- The "OR" Gate

The next gate we are going to learn about is the OR gate. When we say "or", it can sometimes mean "one but not both". For example: "You can go to the movies or to the arcade" would likely not result in you going to the movies AND the arcade. However, there is a slightly different use of "or" that we use in logic, where "or" means "If at least one of the inputs is true, then the output is true". 

For instance: "If you are going to the movies or to the arcade, you should bring your wallet." Now, we can break it down: 

Going to the movies? True. 

Going to the Arcade? False. 

Need your wallet? True! 

Think about the other two possible scenarios. If you go to the arcade and not the movies, you still need your wallet. If you do not go to either, then you will not need your wallet. For computers, they always use "or" like the second example. 

Like the AND gate, the OR gate needs to have at least 2 inputs. The output of the OR gate is equal to zero only when all the inputs are zero. That means, even if a single input bit is equal to one, the output will be one. You can see the symbol used for the OR gate below:

 Below is a truth table for a 2 input OR gate; however, OR gates can take multiple inputs. For example, consider how the table would work if you had three inputs.

Classical Logic Circuits

We can combine individual gates into circuits. One of the simplest circuits we can build is called a half adder circuit. This circuit is going to use the AND and XOR gates to take two bits as input and give their summation as output. First, let's quickly review how addition works in binary. It has many similarities to standard addition!

When we do standard addition, we sometimes have to carry digits. For instance, adding 5+7 gives us 12. Even though we fed in two single digit numbers, our result was two digits. This also happens in binary: if the sum of two digits is greater than 2, we have to carry it to the next column.

Notice that when you do the addition for the first column (on the right-hand side), you only need two pieces of input: the bit from the top number and the bit from the bottom number. However, for every column after that, you need three pieces of input: the top bit, the bottom bit, and another bit that tells you whether anything was carried over from the previous column. We will call this extra bit the carry bit. 

Half Adder Circuit

The half adder circuit is designed to do exactly what you did when you added the right-hand column in the last section. In other words, it takes in two bits (let's call them the top bit and the bottom bit), and outputs their sum (in binary of course!) along with a carry bit to use for the next column. It's called a half adder circuit because it only works for the first column of the addition process. To do the other columns, we would need a more complicated circuit called a full adder.

The half-adder circuit looks like this:

One of the most important tools for understanding logic circuits is called a truth table. A truth table lists all the possible inputs to a circuit along with the corresponding output. Below is the truth table for the half adder circuit, but some of the outputs are missing! See if you can fill in the blanks using your knowledge of classical gates.'

Now let's build this circuit and try experimenting with it!

The tool we are going to use is called Logic.ly, and can be accessed through this link. This is a drag and drop framework which means you can just drag gates from the left-side toolbar to the middle of the page and connect them by clicking on the output of one gate and dragging it to the input of another gate. There are some gates on the toolbar that we have not talked about but you can just ignore them and use the gates we have already learned about. Use toggle switches as inputs to the circuit, and lightbulbs as the outputs. You can turn the switches on or off by clicking on them.

Use your circuit to check the predictions you made in the truth table. Does the output of your circuit agree with your predictions?

XOR gate from NOT, AND, and OR 

One of the interesting things about logic gates is that you can use them to build other logic gates! In this example we're going to use the NOT, AND, and OR gates to build an XOR gate. We can put this XOR gate into a half adder circuit and it should work exactly the same. 

Here is the circuit diagram to construct an XOR gate:

Build this circuit in Logic.ly and fill in the truth table below. Does it do the same thing as an XOR gate?

Next, try replacing the XOR gate in your half adder circuit. Check that you get the same output as before.   

Why might it useful for engineers and computer scientists to be able to build the same gate in different ways?