Multi-qubit States and Entanglement

 Two Qubits

We learned all about the building blocks of quantum information, called qubits. We learned about how quantum computers do things to qubits using quantum gates, like the X, Z, and H gate from the Scratch activity.   

Now are going to learn about what happens when there are two qubits.   

As we'll see, the quantum world becomes much, much stranger when we have two qubits!  

Recall that we could describe one qubit using the Bloch sphere, using an arrow pointing in the direction of our state. For example, |1⟩ on a Bloch Sphere:

When there are two qubits, we might try to draw two Bloch spheres to describe the two qubits. For example we could have two up qubits, 

We could also have two down qubits, or an up and a down qubit.    

But, there are actually more possibilities than just each qubit being separately in one of the states up, down, left, right. These states can only be described in reference to the other qubit. When this happens, we say the two qubits are entangled. 

In this activity, we'll be using another Scratch project,

Just like before, you can drag and drop the gates onto your wire to affect the qubits. Now, there are two qubits in the simulation. There is also a new tool called an "entangler". The entangler is what puts your two qubits into an entangled state. Specifically, it will put the two qubits into an entangled state called a Bell state. 

Pressing the space bar returns your qubits to the entangler, and resets them to the Bell state again.

Bell State

Let's explore the specifics of the Bell state. We'll open up a simulation in Scratch to test out what happens when we make different measurements of a Bell state. Use the simulation to answer the questions below!

The initial set-up is like this:

The box on the left, the entangler, puts the two qubits into the Bell state. The qubits then move along the wires until they are measured. We've chosen to measure both of them the up-down way.

What happens when the entangled qubits are measured in an up-down way?

Does the same reasoning hold if we measure the left-right way?  

Replicate the setup in the figure below in the Scratch simulator see what happens when you measure the qubits in the up-down way.

Now try the setup below and see what happens when you measure both qubits in the left-right way. See if you can think of any rules that explain the measurements you see in different setups.

Rules of Entanglement

Observation 1  

If the top qubit was measured to be in spin-up state then the bottom qubit automatically will fall into spin-up state (provided no gates are acting on either of the wires). 

In the example of the Bell Pair above, if you measure one of the qubits, the other qubit also collapses into the same state as the first qubit (same holds for spin-down). If you added, say an X gate, on the top qubit, then the result of measurement of both qubits will always be different (try this!).

Observation 2

Even when the measurements were carried out in the left-right manner, the outputs of both qubits were still the same as long as no other gates were acting on the channels.

If the top qubit was measured to be spin-right, then the bottom qubit was automatically fount to be in spin-right direction (same holds for spin-left). If you added, say a Z gate, on the top qubit, then the result of measurement (the left-right way) of both qubits will always be different. Try this and confirm it for yourself. 

These observations imply that the direction of measurement does not matter. (Note: A better word for the direction of measurement is measurement basis.)

RULES OF ENTANGLEMENT

When the qubits are entangled, the quantum states of both qubits are always related to each other.

An entangled pair remains entangled regardless of the measurement basis.

Control Gates

Now that we have understood what entanglement is, our goal is to build an entangler. For this, we will need another set of advanced gates. These gates will need at least two qubits to function. 

We will first understand how to use what are called classically controlled gates. Classically controlled gates use a classical bit to determine what gates we will apply to the qubit. 

For example, suppose we have a bit and a qubit. If the bit is measured to be 1, then we apply the gate X to the qubit. If the bit is 0, then we do not apply the X gate. 

You can test out some classically controlled gates using this Scratch circuit simulator. 

Entanglement circuit using IBM Circuit Composer

Now we will use our knowledge of one-qubit gates and the two-qubit control gates to build an entangler (entanglement circuit) using the IBM Circuit Composer. In this activity, you will be building a circuit and noting your observations and results. Follow the steps below to build your first entangler! 

BUILD YOUR FIRST ENTANGLEMENT CIRCUIT

Start a new circuit on IBM Circuit Composer. Give it a name (e.g. entangler) and save the circuit.

Keep two qubits and delete all the extra qubits from the circuit. Reset both qubits to |0⟩. 

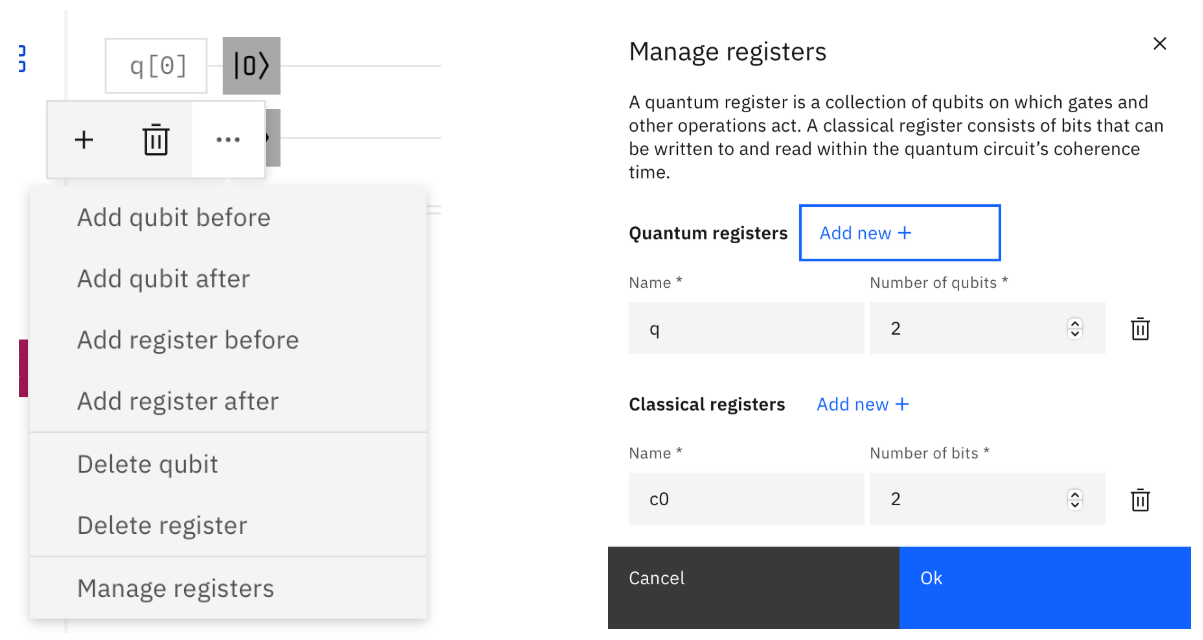
Click on either of the two qubits at the left, then click the three dots symbol to bring up an options menu. Click Manage Registers.

There should already be two qubits, q0 and q1. We'll need one classical bit for each qubit to store the results of any measurements, so set the number of bits in the classical register to 2.

Apply the H gate on the qubit q0. How many states are possible? Note that in the histogram that you see, the x-axis outcomes are written in the format q1q0. What do the measurement probabilities look like? 

Now apply a CNOT gate with q0 as the control bit and q1 as the target bit. The circuit should look as follows:

Apply measurement gates on both qubits. What does the histogram look like?

Run the circuit IBM_QASM_simulator. Once the execution is complete, check the results. How many states are possible? What do the measurement probabilities look like?